Why There Are More .300 Hitters Than .299 Hitters, And Why It Matters

Tobias J. Moskowitz and L. Jon Wertheim, authors of the Freakonomically inclined Scorecasting, explore the peculiar power of round-number milestones and how they affect a ballplayer at the plate.
Adapted from Scorecasting: The Hidden Influences Behind How Sports Are Played and Games Are Won, available on Amazon.
Whether we're buying batteries at Wal-Mart, a fast-food value meal, or even a house, odds are good that the price ends in a nine. We're numb to seeing $1.99 bottles of Coke, $24,999 cars and even $499,999 McMansions on cul-de-sacs. In the case of gasoline, the price even extends to nine-tenths of a cent, say, $2.999 for a gallon of unleaded. This entire concept, of course, is silly. Purchase one gallon of $2.999 gas and it will cost you $3.00. It takes 10 gallons before you'd realize any savings—and it's a mere penny at that—over gas priced at an even three bucks.
The difference between the price ending in a nine and the whole number is virtually meaningless, a negligible fraction of the purchase price. But test after test reveals that there is great psychological value in setting a price point just below a round number. Even among sophisticated consumers able to recognize the absurdity of it all, paying $9.99 is still somehow more palatable than paying $10.00. (Factor in sales tax, and you're paying over $10 in both cases, which makes it more absurd.) Round numbers are powerful motivators—whether it's to hit them or avoid them—in all sorts of contexts.
Devin Pope and Uri Simonsohn, then a pair of Wharton professors, looked at the prices of millions of used cars and found something that was, at once, peculiar and predictable: when the mileage on the vehicles eclipsed 100,000, the value dropped drastically. A car with 99,500 miles may have sold for $5,000. But once the odometer of that same car—identical year, model and condition—rolled over 500 more times and posted 100,000 miles, the value fell off a cliff. Why? Because consumers for a used car set a benchmark of 100,000 miles, and woe unto the seller whose jalopy eclipses that number.
Looking at human behavior, Pope and Simonsohn found that we're slaves to round numbers. Every year more than a million high school students take the SAT, aiming for a round-numbered score as a performance goal. How do we know this? Until 2005, the SATs were scored between 400 and 1600 in intervals of 10. When students posted a score ending in a 90 (1090, 1190, 1290…) they were 20 percent more likely to retake the test than students whose score ended on a round number (1100, 1200, 1300.) The difference in the scores might be as small as a single question—and, according to Pope and Simonsohn, those 10 points do not disproportionately change an applicant's chance of admission. Still, it meant everything to many teenagers (perhaps because they figured schools would have round score cut-offs). And the most noticeable difference in students who decided to retake the test? It was between those scoring 990 versus those scoring 1000.
Some of the most arresting research came when the researchers considered the behavior of Major League Baseball players. Baseball, of course, is flush with "round number targets." Pitchers strive for 20-win seasons. Ambitious managers challenge their teams to win 100 games. Batters try like hell to avoid the notorious "Mendoza line" of a .200 average. But no benchmark is more sacred than hitting .300 in a season. It's the line of demarcation between All-Stars and also-rans. It's often the first statistic cited when making a case for or against a position player in arbitration. Not surprisingly, it carries huge financial value. By our calculations, the difference between two otherwise comparable players, one hitting .299 and the other .300, can be as high as two percent of salary, or, given the average major league salary, $130,000. (Note that though the average MLB salary is $3.4 million, it's closer to $6.5 million for players batting in the .300 range.) All for .001 of a batter's average, one extra hit out of 1,000 at-bats.
Given the stakes, hitting .300 is, not surprisingly, a goal of paramount importance among players. How do we know this? Pope and Simonsohn looked at hitters batting .299 on the final day of each season from 1975 to 2009. One hit and the players could vault above the .300 mark. With a walk, however, they wouldn't be credited with an at-bat or a hit, so their average wouldn't budge. What did these .299 hitters do? They swung away. Wildly. We looked at the same numbers and here's what we found. Players hitting .300 walked 14.5 percent of the time and players hitting .298 walked 5.8 percent of the time, but in their final plate appearance of the season, players hitting .299 have never walked. In the last quarter century, no player hitting .299 has ever drawn a base on balls in his final plate appearance of the season.
The following chart highlights these numbers. Note that it spikes like the EKG of a patient in cardiac arrest.
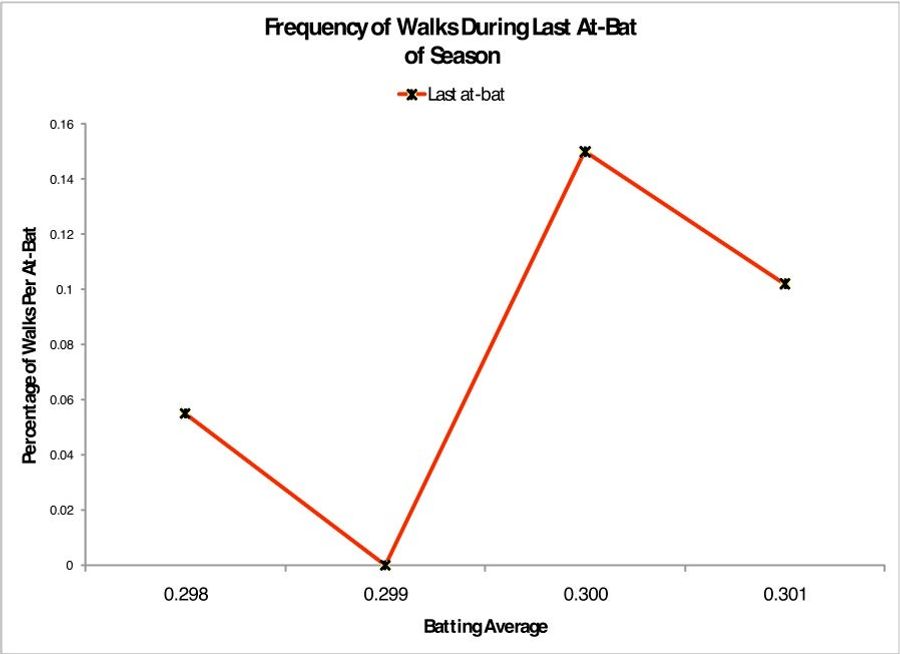
If we look at the likelihood of a walk for hitters just below .300 versus just above .300 before the last game of the season—or even during the last game but before the last at-bat—we don't see any stark differences. But for that last at-bat, when they're desperate to reach that .300 mark, they refuse to take a base-on-balls, swinging away to get that final hit that will put them over the line. Yet before the last game, .299 hitters actually walk slightly more than .301 hitters.
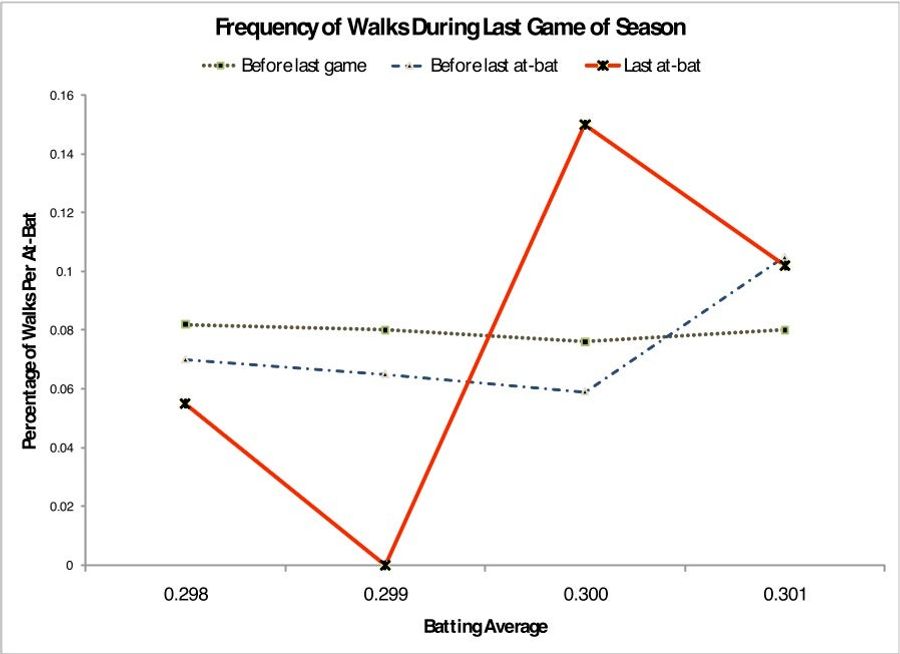
What's more surprising is that when these .299 hitters swung away, they've been remarkably successful. According to Pope and Simohnson, in that final at-bat of the season, .299 hitters have hit almost .430. In comparison, in their final at-bat, players hitting .300 have hit only .230. (Why, you might ask, don't all batters employ the same strategy of swinging wildly, given the success of .299 hitters? Does this not indict their approach the rest of the season? We think not. For one, these batters never walk, so their on-base percentages are markedly lower than more conservative hitters. Also, if every batter swung away liberally throughout the season, pitchers likely would adjust accordingly and change their strategy to throw nothing but unhittable junk.)
Another way to achieve a season-ending average of .300 is to hit the goal and then preserve it. Sure enough, players hitting .300 on the season's last day are much more likely to take the day off than are players hitting .299. Even when .300 hitters do play, in their final at-bat they are substituted for by a pinch hitter more than 34 percent of the time. In other words, more than a third of the time, a player hitting .300—an earmark of greatness—will relinquish his last at-bat to a pinch hitter. (Hey, at least his average can't diminish.) By contrast, a .299 hitter almost never gets replaced on his last at-bat.
With the .299 players swinging with devil-may-care abandon and the .300 hitters reluctant to play, you probably guessed the impact: After the final game of the season, there are disproportionately more .300 hitters than .299 hitters. On the second-to-last day of the season, the percentage of .299 and .300 hitters is almost identical—about 0.80 percent of players are hitting .299, vs. 0.79 percent of players hitting .300. However, after the last day of the season the proportion of .299 hitters drops by more than half to less than .40 percent and the proportion of .300 hitters rises to 1.40 percent, more than a twofold increase.
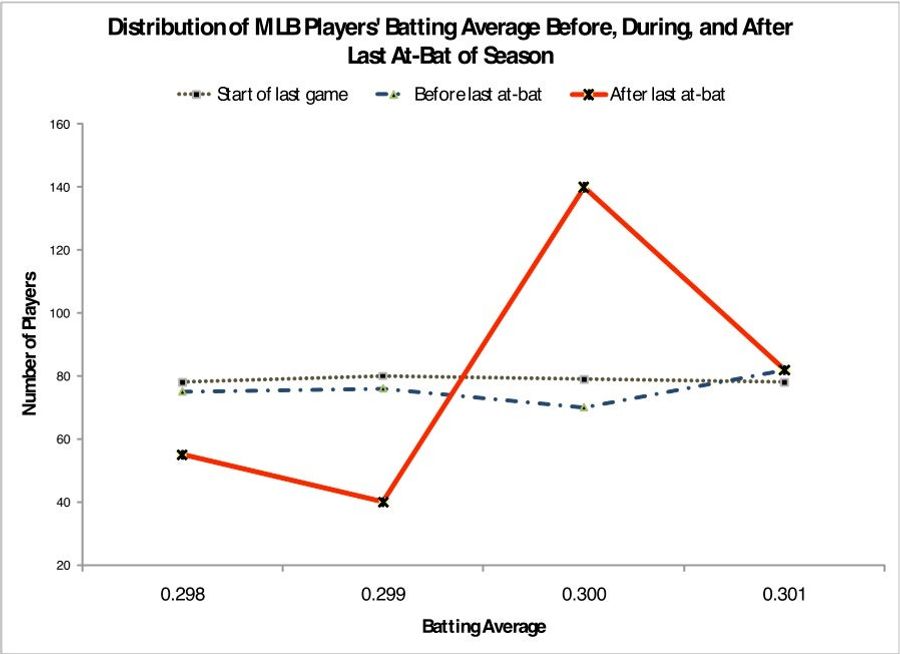
Looking at the Pitch f/x data, which tracks not only the location but the speed, movement and type of every pitch thrown, we found that neither the location, type of pitch, speed, movement, or any measurable attribute of pitches was reliably different when a pitcher faces a batter with a batting average just below the .300 mark at the end of the season. Pitchers are either unaware that batters are just shy of .300 or don't care—they pitch the same way to the .299 hitter as they do to the .300 batter.
Data, however, tells us what isn't the same: batters hitting .299 swung more liberally, taking fewer called strikes and balls but having more swings and misses, even when facing three balls in the count. In their last at-bat they did everything possible not to draw a walk. As a result, they got more hits. In comparison, .300 batters drew many walks and did not swing on three-ball counts.
Of course, the .300 mark isn't the only round number players strive to attain. The century mark for RBIs is another coveted goal, and so we see the same pattern, with many more players than expected ending the season with 100 RBIs, and far fewer ending with 99. And again, the differences are mostly generated from the last game and even the last at-bat of the season.
The same pattern emerges for those players with 19 or 29 (or 39 or 49) home runs. Players do everything possible to move up to the next round number. So on their last at bat they swing for the fences. We see a disproportionate number of players hitting 20 or 30 (or 40 or 50) home runs compared to 19 or 29 (or 39 or 49) home runs, often thanks to that last at-bat.
And, like achieving a .300 batting average, the difference between hitting 99 and 100 RBIs, or 29 versus 30 home runs, or 19 versus 20 wins as a pitcher, is worth real money in terms of future salary. Teams, owners, and GMs clearly value the higher round numbers. In this respect, players may be acting economically rational, responding to the incentives provided by teams to do everything they can on their last at-bat to reach those numbers.
We also noticed something else. The numbers above and those from the study only looked back to 1975, when free agency existed. We took a look at the data going back to the early part of the 20th century until the early 1970s, before free agency. We found that the number of players hitting round numbers exactly, relative to those just missing them, diminished significantly before the free agent era. Another clue that players are responding to the financial lure of round numbers.
The puzzle is why the Republic of Sports values round numbers so much. One might even contend they should value round numbers less because they are being gamed by the players. Is the extra salary paid for a .300 hitter worth so much more when it is largely determined by a single at-bat on the last play in what was likely a meaningless game at the end of the season? Or when it was attained sitting out the last game to ensure the player's average didn't go down? The difference between a .300 and .299 hitter is negligible—one misdirected ground ball, one blooper into short center field, one random bounce, one generous judgment by an official scorer over the course of a season. We would argue .300 and .301 hitters are overvalued, and .298 and .299 hitters are undervalued. A hedge fund manager would spot this as an "arbitrage"opportunity, and would unload the overvalued asset and buy the undervalued one. A savvy GM might consider doing the same: trading the .300 or .301 hitter for a player who hit just under .300, saving many thousands without affecting the hitting performance of his lineup.

Tobias J. Moskowitz is the Fama Family Professor of Finance at the University of Chicago. He is the winner of the 2007 Fischer Black Prize, which honors the top finance scholar in the world under the age of 40. L. Jon Wertheim is a senior writer for Sports Illustrated, a recent Ferris Professor at Princeton, and the author of five books, including Strokes of Genius: Federer, Nadal, and the Greatest Match Ever Played. You can buy Scorecasting .
Top image by Jim Cooke
Related
Next Big Stars in WWE: Watch These 2026 Breakout Stars
The AFC Is Wide Open Heading Into Week 15
Kansas City Chiefs Need Offensive Changes This Offseason
Why Kansas City Chiefs Aren't Done Yet Despite 6-6 Record
NBA Best Bets Today: Sunday Dec. 7th Top NBA Picks
- Top 10 NFL Player Props for Week 14: Best Bets and Expert Picks
- College Football Conference Championship Best Betting Picks, Predictions
- UFC 323 Betting Picks: Best Bets for the Final ESPN Pay-Per-View
- NBA Best Bets Today: Top Betting Predictions for Friday Dec. 5th
- Washington Capitals vs. Anaheim Ducks December 5th Betting Picks, Predictions
- College Basketball Weekend Bets: Gonzaga, Duke, and Michigan State Predictions
- Cowboys vs Lions Thursday Night Football Betting Prediction: Week 14 Bet Picks












