This New NBA Stat Is A Huge Step Forward For Basketball Analysis

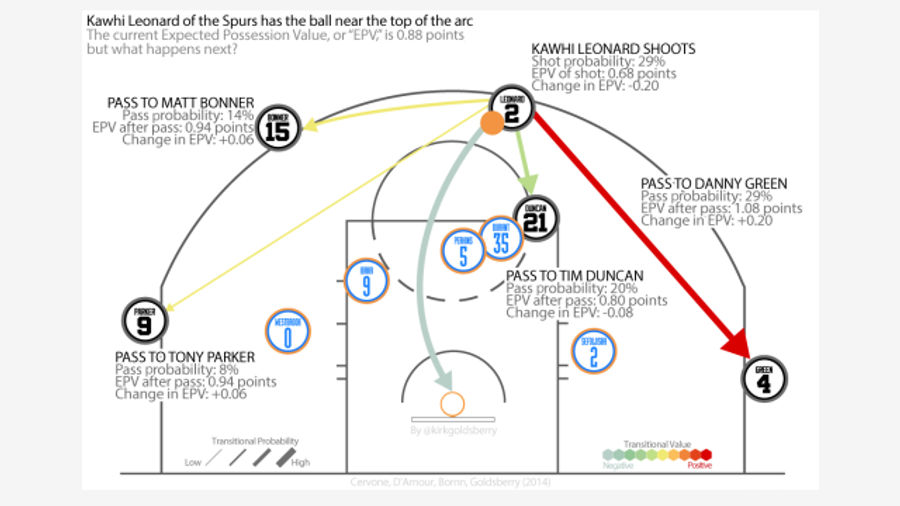
This morning on Grantland, Kirk Goldsberry introduced the stat Expected Possession Value Added (EPVA), which he developed with some colleagues as part of a Sloan Conference paper. EPVA still needs some work, but it may represent an enormous development in NBA analysis. Here's why.

There's a whole breed of advanced metrics* dedicated to calculating the impact of individual plays on game outcomes. For MLB we use Run Expectancy (RE24) and for the NFL we use Expected Points Added (EPA), both of which serve as the basis for the extremely useful stat Win Probability Added (WPA). However, baseball and football are structured as discrete events—a single pitch leads to a single swing, a single snap leads to a single pass—while basketball is a continuous action sport. This greatly complicates this sort of analysis: If a team has a possession with a post up, a kick out, a swing pass, and a corner three, how do you assign credit to all the players involved?

Kirk Goldsberry and his Harvard colleagues seem to have made major progress on this problem—for offense, at least—with a model based on the new data from the SportVU player-tracking cameras. EPVA measures the expected points value (EPV) over the course of a possession, based on the position of the ball, the offensive players, and the defensive players, and then assigns shifts in this expected value to the actions of individual players.

Here's an example, from the final play of Spurs-Cavaliers on February 13th, 2013:

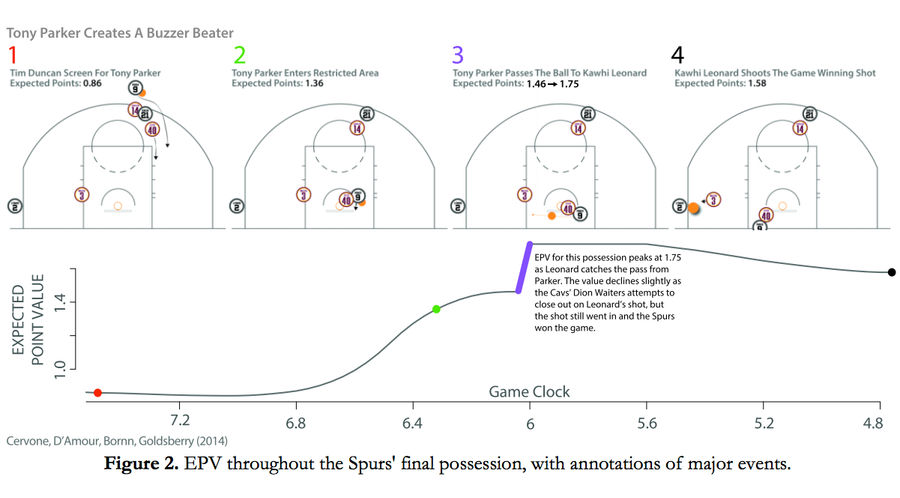
The line graph on the bottom shows the expected point value over the course of this possession, which starts at 0.97. A Tim Duncan screen sets up a Tony Parker to drive, slightly decreasing EPV as he drives right at a defender (Zeller)—a quintessential Parker move—but then increasing EPV once the point guard enters the paint. EPV spikes as Parker kicks it out to Kawhi Leonard in the corner. Leonard will eventually shoot, but before he does the defender attempts to close, so EPV slightly declines. He nails the shot for the buzzer beater. Parker starts with the ball at a 0.97 EPV and has increased it to 1.75 when Leonard takes his pass, so his expected possession value added (EPVA) for the play is +0.78. That's how much value was added from the time Parker starts the possession until the point that the ball is in Kawhi Leonard's hands, so even if Leonard missed, Parker would still get +0.78.

There are plenty of potential tweaks to how this EPVA assignment should work. Why doesn't Duncan get any credit for the screen? Is it possible to assess the quality of Parker's pass beyond the fact that he made it? What about the quality of the defense? What about the shot clock? This is still a work in progress, but the core idea—that the impact of individual actions and decisions can be quantified based on spatial data—is extremely powerful.

In 2012-13, only 13 arenas had the SportVU tracking cameras. Here are the top five players in EPVA added per game, based on this incomplete sampling:

Chris Paul (+3.48) – this doesn't count any home games!

Dirk Nowitzki (+2.60)

Deron Williams (+2.52)

Steph Curry (+2.50)

Jamal Crawford (+2.50)

Here are the bottom five:

Ricky Rubio (-3.33)

Kevin Love (-2.38)

Russell Westbrook (-2.07)

Evan Turner (-1.90)

Austin Rivers (-1.84)

These charts point to what might be the biggest conceptual problem with this statistic—by its very nature, it gives more opportunities for point guards to gain or lose EPVA, so it would be nice to a positional adjustment that accounts for that. That's the sort of thing that can be worked out in time, though. The important thing is that for the 2013-14 season, all NBA arenas are equipped with SportVU cameras. This work, and the analysis it can yield, is just getting started.

*All based on Markov models, if you want to classify them.

[ Grantland, here's the paper]