The Competitive-Balance Argument Against Paying Athletes Is Bullshit

High on the list of myths thrown out as excuses to delay or prevent the advent of pay-for-play is that the price-fixing engaged in by the 351 schools in Division 1, and especially the now 128 schools in FBS who play football, is necessary to ensure competitive balance across the sport.
This is a useful myth. It appeals to fans of all stripes, because part of us wants to think of college sports as being very egalitarian, that everyone starts off with the same chance to win the championship. Sure we have to ignore the cognitive dissonance from the fact that we all know there are perpetual powerhouse and perpetual creampuffs, but the myth makes us feel good. It was a driving force behind the 2011 override of efforts to increase the maximum scholarship allowed by the NCAA-wide price-fixing agreement, whereby schools collude to set the wages of their athletes at below-market rates.
When faced with the possibility of having to compete more vigorously for talent, some schools threw up the competitive balance argument and succeeded in scuttling the planned increase. Among those schools were:
Boise State: "Boise State believes the following: … [The rule change that would have allowed $2,000 stipends] creates an unfair playing field between institutions. It expands the divide between the 'have's' and 'have not's.' It creates a recruiting advantage for those that can afford it and puts those that can't at a disadvantage."
Marshall: "The institution is not in a position to fund the additional costs associated with the miscellaneous expense. Many institutions are likely to be in the same position which would create a competitive advantage for those institutions who had large budgets."
Tennessee Tech: "It also will lead to unlevel playing fields as some institutions will bow to pressure; or in some cases have assets that will allow student-athletes across the board to receive the other countable aid in order to be more competitive athletically." (For people who like examples of casual stereotyping, Tennessee Tech also explained that providing athletes with stipends was a bad idea because: "It seems most dubious to give some student athletes what amounts to 'tattoo money'…")
It is not just college sports administrators who believe this. The editorial board of the Wall Street Journal: "The rules are meant to protect the school's reputation, keep kids out of trouble, and maintain competitive balance among schools."
Just last week, Baylor University President Ken Starr submitted testimony to Congress to this effect: "If antitrust principles and collective bargaining eliminate pro-competitive limitations on payments and benefits, there may literally be no 'competitive' intercollegiate sports."
In past articles (see here and here, as examples), I've explained how little factual content there is to the claim that fixing prices will enhance competitive balance in a system where the revenue-generating value of talent differs so dramatically across the full spectrum of FBS schools. In particular, my own research in 2011 showed that of the 1,000 top recruited athletes over a decade, 99.3 percent went to power conference schools. As you'll see below, the truth is that the current rules seem to lock in imbalance, and prevent would-be upstarts from building recruiting momentum.
I'm not alone in this conclusion. Economists are not generally a group of people who reach an easy consensus, but in this case there are multiple published articles that conclude that, rather than improving competitive balance, the NCAA's price-fixing scheme either has no effect on balance, or makes it worse. These include:
Baird, Katie, "Dominance in College Football and the Role of Scholarship Restrictions," Journal of Sport Management Vol. 18, No. 3 (2004),:
This suggests preliminary support for Rottenberg's invariance principle: where talent goes (and thus competitive balance) is invariant with the degree of restrictions over player pay. No statistically significant change in competitive balance has occurred in college football since greater restrictions over paying athletes have been introduced. ... In short, little evidence supports the claim that NCAA regulations help level the playing field; at best they appear to have had a very limited effect, and, at worst, they have served to strengthen the position of the dominant teams.
Depken, Craig A. and Dennis P. Wilson "The impact of Cartel Enforcement in Division I-A Football," in Fizel, John and Rodney Fort, "Economics of College Sports," 2004
NCAA [recruiting] sanctions tend to reduce competitive balance, on average. ... Our pooled results do support the claim that NCAA enforcement may have the unintended consequence of reducing competitive balance.
Eckard, Woodrow E., "The NCAA Cartel and Competitive Balance in College Football," Review of Industrial Organization 13, 1998
The NCAA regulates college football player recruiting, eligibility, and compensation. The economic theory of cartels suggests that one consequence may be reduced competitive balance. The enforced restrictions inhibit weak teams from improving, and protect strong teams from competition. A 'stratification' is implied which should be evident over time as less 'churning' in national rankings and conference standings, and fewer schools achieving national prominence. I test this general hypothesis by comparing various competitive balance measures for about 25 years before and after NCAA enforcement began in 1952. The hypothesis is supported by all measures at both the national and conference levels.
Fort, Rodney "Sports Economics" (textbook 2nd Edition 2005, 3rd edition now available)
Competitive imbalance exists in college sports ... Just as with pro leagues, a cursory analysis reveals that none of the restrictions on players actually have anything to do with competitive imbalance. Instead, they transfer value produced by players away from the players and toward the athletic department. (p. 492)
Interestingly, many believe that these recruiting restrictions create a level playing field that enables poorer athletic departments to compete with richer ones for talent. Nothing could be farther from the truth. Instead, these restrictions entrench power at departments at the top end of the winning percent distribution.
Athletic directors and NCAA executives alike argue that competitive balance would be harmed if competition were to dictate college player compensation. However, the invariance principle suggests that competitive balance is invariant as to who gets to keep the MRP of players. Under the amateur requirement, players simply earn less but go to the same schools they would otherwise choose.
Peach, Jim, "College athletics, universities, and the NCAA," The Social Science Journal 44, 2007
Third, there is little evidence that the NCAA rules and regulations have promoted competitive balance in college athletics and no a priori reason to think that eliminating the rules would change the competitive balance situation.
Sutter, Daniel and Stephen Winkler, "NCAA Scholarship Limits and Competitive Balance in College Football," Journal of Sports Economics Vol. 4, No. 1 (February 2003), pp. 3-18:
Conventional wisdom holds that parity is greater in college football today than ever before and that scholarship limits have fostered today's competitive balance. A variety of measures indicate that the stylized fact is false; indeed, several measures indicate that college football has been less balanced since the imposition of scholarship limits. ... An examination of the NCAA vote reducing the scholarship limit to 85 finds that recent success on the field made schools more likely to vote for the lower limit, but success over the entire postwar period did not affect voting. These results support the interpretations that the limits were to protect incumbent football powers or perhaps to protect rents generated by amateur status; the interpretation that weaker schools voted to level the playing field is rejected.
These findings are robust across these many studies—fixing prices for athletes does not help balance college sports, but college administrators and even members of Congress keep throwing out the claim that it does. So in the hope that massive amounts of evidence can overcome raw, unsupported assertion, I sat down with several years of recruiting data and asked a simple question: How much less balanced are the results of college football recruiting than they would be under an actually balanced system?
I got the idea to do this analysis from reading this article by Kevin Trahan, which looked at my own testimony before Congress last week. In it, Patrick Hruby and Adam Jacobi were quoted as echoing my point that there is no current competitive balance, and Trahan backed that up with some excellent raw data.
Trahan's article pointed me to the 24/7Sports website, which has 13 years (2002 through 2014) of complete recruiting data for all or virtually all of FBS, plus the upper end of FCS football for some years. If you want to focus on the most relevant question of competitive balance in the recruiting of football athletes, the place to look is in the recruiting of football athletes. Looking at the game results is also useful (and trust me, it does not show balance, unless you think the fact that a MAC team has never won a national championship during the Scholarship Agreement era—1956 to the present—is evidence of balance), but game results can include upsets, where a team built through clearly inferior recruiting efforts defeats a team with far more recruiting success. (To be clear, as Joel Maxcy reminds me, recruiting outcomes are great predictors of on-field success in general. When a non-power conference team beats a power-conference team, we call it an upset; we rarely, if ever, call the reverse an upset. That's a good sign we know that there isn't balance across conferences). Still, I wanted to focus on recruiting itself.
With those inputs in hand, I set out to test whether and how balanced college football recruiting is.
I decided there are really two dimensions to test to see if college football recruiting is at all balanced. The first is to test whether, from year to year, the same schools tend to do better and the same schools tend to do worse, in terms of attracting the best recruits. If you follow college football even a tiny bit, you know that this is true. You know Alabama consistently lands five- and four-star recruits in large numbers and Bowling Green does not. In other words, you already know there is virtually no competitive balance in football recruiting.
But I'm here to be scientific about this and so I used a measure of balance called Spearman's Rank Correlation Coefficient, as suggested by Joel Maxcy (who used recruiting rankings in his recent paper on coaching performance). This coefficient tests how likely it is for a team that landed a highly regarded recruiting class in one year to land another highly regarded class in the following year. The coefficient can range from -100 percent (meaning that whenever you do well in one year, you tend to do much worse the next) through zero (where one year and the next are utterly unrelated) to 100 percent, which would occur if, year after year, your rank in the pecking order remained the same—the best school in one year remained the best in the next, the second best remained second best, etc.
Can you guess the results? Here are the last six years' worth of scores:
| 2009 | 2010 | 2011 | 2012 | 2013 | 2014 |
| 87.5% | 92.1% | 90.9% | 92.2% | 93.5% | 93.0% |
Rather than hovering near zero, where there's no relationship between a school's success from one year to the next, the numbers instead are on the imbalanced end of the range of possible values, and getting less balanced over time. Again, this should not surprise anyone with even a smattering of actual knowledge of football recruiting, but that doesn't stop all sorts of people form claiming that price-fixing must remain in place or the same teams will get all the best recruits, year after year. As shown above, they already do.
I also wanted to see what the Spearman coefficient would look like if this weren't the case, so I created a set of random recruiting results. I wanted two things—I wanted each year's results to be independent of the next, and I also wanted lots of schools to do similarly each year.
I picked a specific form of a random distribution, known as a Chi-Squared distribution.1 This is what six years of random, balanced results look like:
| 2009 | 2010 | 2011 | 2012 | 2013 | 2014 |
| -6.8% | 13.2% | -0.3% | 13.5% | 15.0% | -31.2% |
In some years, previous success has a small negative impact on the next year's success; in others, it has a small positive. But there is no clear pattern and it's very clearly different from real life, in which success from year to year is highly likely and getting increasingly likely over time.
That was Dimension 1. My second dimension was simply to test how concentrated recruiting points were. In theory, we could see the same teams having the same results in terms of their recruiting rank (i.e., Alabama could always be first), but they could be very closely clustered—10th place might just be a smidge below first, etc. Or, there could be big differences between even first and second places, second and third, etc. In other words, I wanted to see just how big the class of elites really is, and where and how wide the gaps are.
To test this, I needed a measure of concentration, which would tell me how many of the recruiting points were clustered in the hands of a few elite schools or spread out among any schools. The more spread, the more balanced.
At Maxcy's suggestion, I used what's called coefficient of variation. This is a pretty simple statistic, formed by taking the standard deviation of a series (a measure of the spread of a data series) and dividing by its mean (i.e., the average). Numbers below 1 tend to be a sign of higher concentration (in this context it would mean that more of the recruiting wins of the best athletes were focused on a small number of elite schools) and numbers above 1 tend to be a sign of more dispersal (lots of highly rated recruits going to all sorts of schools). Most importantly, you can compare coefficients of variation across different years and different outcomes and whichever is lower is a more concentrated (imbalanced) outcome.
Here is how the last six years looked in real life:
| 2009 | 2010 | 2011 | 2012 | 2013 | 2014 |
| 0.59 | 0.53 | 0.76 | 0.51 | 0.45 | 0.43 |
In other words, the data are relatively concentrated, indicating that a small number of teams are getting the lion's share of the best athletes, and with the exception of 2011, the tendency is getting worse—competitive balance is actually getting worse, not better.
Remember my random sample, which I set up so that most of the data would be clustered toward the low end? This is how that random simulated recruiting market worked out on this measure:
| 2009 | 2010 | 2011 | 2012 | 2013 | 2014 |
| 1.39 | 1.38 | 1.43 | 1.20 | 1.38 | 1.70 |
With a synthetic data set based off of a random distribution of talent, the scores are all above 1, and there is much less of a trend to them. This is what a balanced, unconcentrated outcome might look like, as opposed to the highly concentrated outcome we see in real life. For people who prefer data graphically, the below shows you, quite clearly, how different real life is from anything that can be described as balanced:
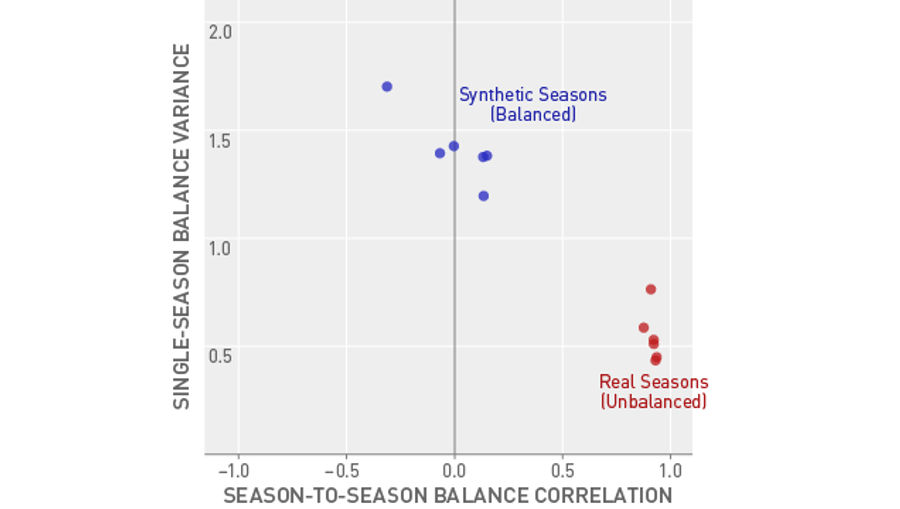
Remember, in this chart, the higher on the vertical (y) axis you are, the more balanced any one season is, and the more to the left on the horizontal (x) axis you are, the more balanced you are from season to season. The real world data are low on the y-axis (hence, imbalanced) and also large on the x-axis (also imbalanced).
I have six more years of earlier data (I have 13 years in total, but to do the Spearman Coefficient for any one year requires a peek at one year's earlier numbers so it takes 13 years of data to do 12 years of calculations). I added those to my analysis and they show basically the same results—balance was better at the beginning of the data (2002) than in the middle (2008) and both were better than the end (2014). The Spearman Coefficient looks like this if we focus in on the changes over time by using a non-zero origin point:
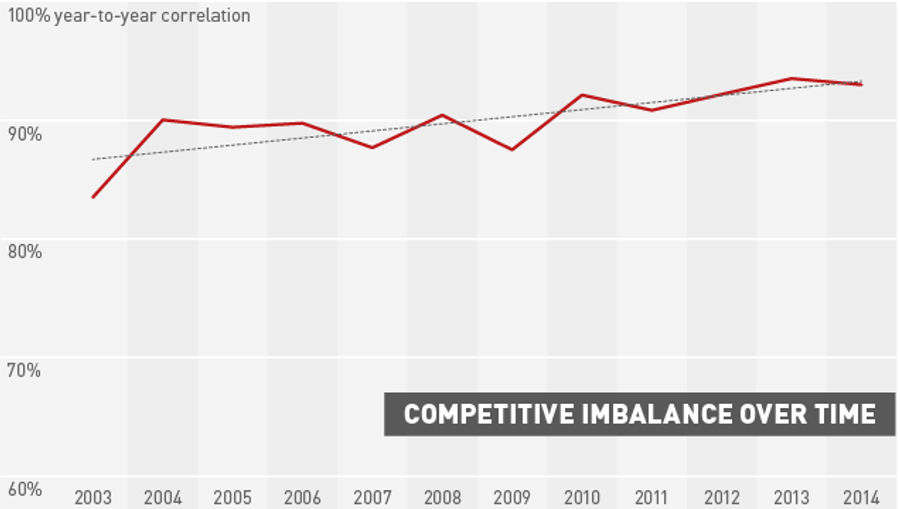
(For the graphics nerds out there, I realize I've used a non-zero axis on this chart. The zero axis is also informative—it shows that competitive imbalance is basically as high as it can possible get. In this case, the non-zero axis lets me show this and also show the trend is getting worse.)
With the new data added, the spread between what balance would actually look like and the imbalanced reality is only further emphasized:
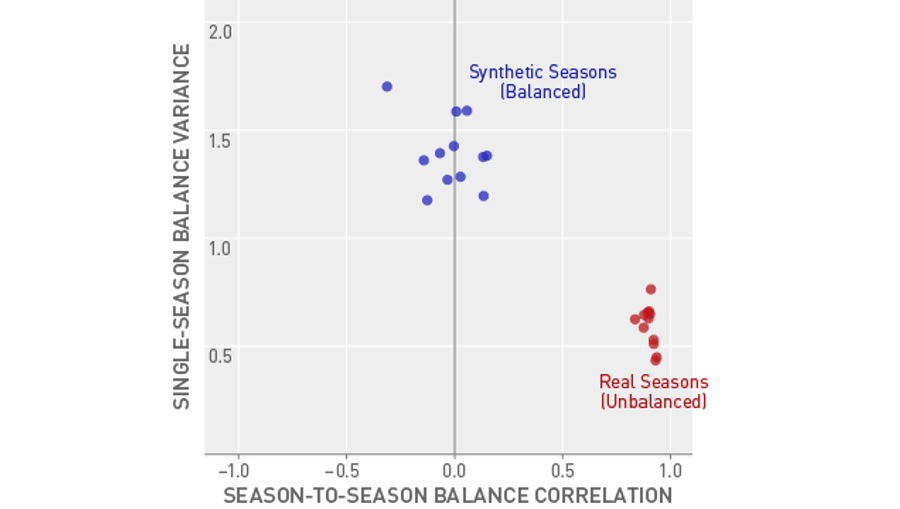
To the surprise of no one who knows the industry, college football recruiting is anything but balanced, and it is getting increasingly imbalanced over time.
As expected, a rigorous statistical analysis confirms what every fan of any powerhouse team already knew: Teams with recruiting success tend to remain successful year after year and teams without much success tend to remain unsuccessful. Fixing the price of a year of a college athlete's service to be comparable across all schools does not result in anything like competitive balance, and statistically, the level of imbalance has been growing over the last six years. It's time to stop using that as an excuse why college football should be allowed to collude its way out of paying market rates for talent.
Why the balance has been getting worse is open for consideration. One obvious candidate theory is that as the power conferences' resources grow, their ability to use money to gobble up talent grows, too. Some people might point to that conclusion and argue that's why price-fixing is needed, to prevent power schools from using their money to imbalance the recruiting market. But that's the precisely wrong conclusion. These data show that the money flowing in already correlates almost perfectly with year-to-year recruiting success. The money-yields-talent equation is supported despite the price-fixing. Sports economists already knew this—as early as 1956 Simon Rottenberg explained that talent will flow to where it is most valued.
To the extent you like your truth from college sports administrators rather than economists (leaving aside that questionable choice!), consider the similar conclusions of Big 12 Commissioner Bob Bowlsby: "The concept of competitive equity through rules management is largely a mirage. It hasn't worked at any level."
How about getting the truth from Jeffrey Kessler, the famous antitrust attorney who led the movement to get free agency in the NFL: "Anyone who thinks that a small school from the lower ranked conferences competes for the same football players as Alabama, or Auburn, or Texas, or Michigan, or Ohio State, either knows nothing about college football or is a fool."
But how would things look under a pay-for-play model? Would the imbalance actually get worse?
Maybe not. If anything, the economics of price competition argue that as you let schools use money directly as a tool in attracting talent, you may empower mid-level schools to splurge on a would-be starter who might otherwise accept an offer at a top-tier school and end up riding the bench. When stars and benchwarmers all get the same compensation package, there's no way for a smaller school to show they really want a player much more than the big school, which is free to stockpile talent. Both schools can claim they want the player, both can send 700 letters in one day, etc. The best way to show you mean business and that the other school is just engaging in what economists call " cheap talk" is price competition.
So when you buy into the myth that price-fixing helps balance college football, you're actually helping prevent that balance from emerging. Stop defending price fixing and you'll let Bowling Green show that four-star nose tackle how much more valuable he is to the Falcons than he is to Alabama's bench.
Acknowledgements: I got great assistance from three professors of sport management/economics. Diane Bruce Anstine, Rod Fort, and especially Joel Maxcy. Maxcy basically suggested both of the metrics I used here and then vetted a near-final draft of this article. So thanks, Joel, for letting me steal your knowledge for my own publishing glory.
Charts by Reuben Fischer-Baum
Andy Schwarz is an antitrust economist and partner at OSKR, an economic consulting firm specializing in expert witness testimony. Follow him on Twitter, @andyhre.
1Gory methodological details: You maybe remember the Normal distribution from your statistics classes. The Chi-Squared is what you get if you generate a series of Normally distributed numbers and then square them. Because they are squared, they can never be negative, and they tend to cluster around the low end, but have a small probability of very large numbers. For the curious, I used a standard normal distribution with mean of zero and standard deviation of 1 and then just squared the results. I then took the total number of recruiting points from real-life for each year and spread them out across the randomized results so that the random numbers totaled to the same value as the real-life results.
Related
The Three Biggest 2026 NBA All-Star Starter Snubs
Why John Harbaugh Is Exactly What the New York Giants Needed
Why the Detroit Lions’ Drew Petzing Hire Makes No Sense
- Sunday January 18th College Basketball Betting Picks, Predictions
- Houston Texans vs. New England Patriots NFL Playoffs Betting Picks, Predictions
- NFL Divisional Round 2026 Best Bets, Picks, Predictions
- Buffalo Bills vs. Denver Broncos Divisional Round Betting Picks
- Top NBA Betting Picks Tonight: Clippers-Raptors, Wolves-Rockets, Wizards-Kings
- Thursday Jan. 16 NHL Betting Picks: Lightning vs. Blues, Panthers vs. Hurricanes
- Thursday NBA Betting Picks: Three Best Bets Before a Big Sports Weekend












