The NFL's Dumbass Deflategate Science Report Is A Feature, Not A Bug

Last night, a mountain of documents and transcription emerged from Tom Brady’s late June appeal hearing before Roger Goodell. It’s been a circus, with a series of insults, emails, and sneaker requests to Tom Ford pouring out of the file cabinet, but the testimony most relevant to the case circles back to whether or not the NFL has any statistically compelling evidence against Brady.
The NFL’s Mock Trial Club courtroom is an easy target for derision, a mess of every meathead/empty-suit pathology that infects the league, laying down cover fire for hilarious decisions that are typically overturned upon any reasonable pushback. But it also does something funny to the process, codifying judgements into legal framework, thereby creating a burden of evidence that requires something like statistical proof beyond the overwhelming circumstantial bits that show Brady is, very obviously, guilty as shit. The NFL’s courtroom is so slanted that it’s practically made bad, biased science a requirement to completing the process. And so we get the Exponent report, a document that cost the NFL $600,000 dollars to produce. Here is analysis of the statistical arguments found in the transcriptions.
Patriots Argument
The beginning of the Exponent report contains a statistical model that shows a 0.4% chance (p-value of 0.004) of the Patriots’ ball deflation occurring naturally. This sounds very bad! The result is prominently quoted in the Wells report, and it’s what the Patriots attempted to refute with testimony from Professor Edward Synder of the Yale School of Management. The professor’s slides were not released, but we can go over the arguments he makes, which are compelling. (Appeal p 160-188)
Here’s what we know: The difference between the measured pressure of the Patriots’ and Colts’ footballs was roughly 0.7 psi when they were measured at halftime, according to the Exponent report. When the footballs were taken inside to the locker room to be measured at the half, the Patriots footballs were measured before the Colts footballs. During this time, the Colts footballs warmed up and the pressure rose accordingly, as dictated by the Ideal Gas Law. It’s not known exactly when the footballs where measured, but the Patriots footballs were measured first, then (it seems) the Patriots footballs were re-inflated, and then finally (it seems) the Colts footballs were measured near the end of halftime. (We can probably assume this was right at the end of halftime, because only four of the 12 Colts footballs were measured.) The Exponent report contains plots of how much the pressure increases over time under various scenarios of football wetness.
In short, this means that when the balls were measured is a very big part of understanding how they compare to each other. Here’s how Snyder explained this to Goodell:
Q. Okay. So let’s go, let’s start with your slide deck. The first slide shows your three key findings. And if you could just sort of walk the Commissioner through each of the three key findings that you made and that we will elaborate on.
A. So first finding is that their analysis of the difference in differences, the analysis of the pressure drops and the difference in the average pressure drops is wrong because Exponent did not include timing and the effects of timing in that analysis.
Secondly, Exponent looked at the variation and the measurements between the Patriots’ balls and the Colts’ balls at halftime. They compared the variances. And despite conceding that there was no statistically significant difference between the two, they went ahead and drew conclusions, but those conclusions are improper.
And, last, and this goes to the issue of alternative assumptions, as well as error, if the logo gauge was used to measure the Patriots’ balls before the game, then given what the framework that Exponent provides us with scientifically, and if the analysis is done correctly, eight of the eleven Patriots’ balls are above the relevant scientific threshold.
There’s a lot here, but the most blatant point is the issue of timing. Here’s a chart from the Exponent report itself:
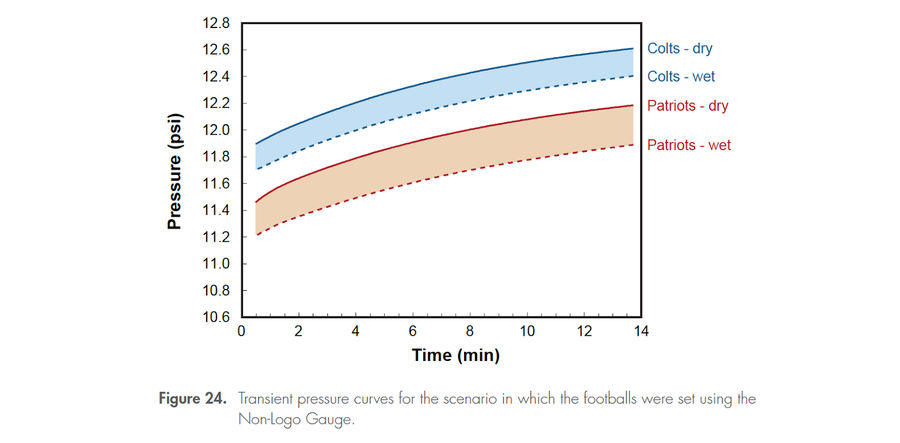
There are several curves on the graph; however, the pressure increases roughly 0.6-0.7 psi during halftime for all of them. Therefore, based on timing, it is expected that the Colts’ football deflation should be 0.3-0.4 psi less than the Patriots’ balls. The Patriots’ footballs might have been wetter than the Colts’ because the Patriots’ had the ball at the end of the half, so that could have caused another 0.1 psi difference. Finally, the referee said the Colts’ footballs could have been 13.1 psi rather than 13.0 psi before the game and this is another potential 0.1 psi adjustment. Overall, adjustments exist from 0.3-0.6 psi which shrink the Patriots-Colts difference of differences from 0.7 psi to 0.1-0.4 psi. Not surprisingly, this greatly changes the statistical p-value the Exponent model gives:
Adjustment (psi) | p-value |
0.0 | 0.004 |
0.1 | 0.010 |
0.2 | 0.026 |
0.3 | 0.062 |
0.4 | 0.140 |
0.5 | 0.290 |
0.6 | 0.540 |
A p-value above 0.05 is not considered statistically significant and a p-value above 0.1 is considered to show no evidence at all against the null hypothesis. Therefore, with an adjustment of 0.3 psi or larger there is no statistically significant evidence that the Patriots footballs were deflated. This is the core of the Patriots’ statistical argument.
NFL Cross Examination of Patriots Argument
Exponent gave several criticisms of this argument, none of which were very good. First, Exponent had a technical criticism of this analysis because the Patriots (or equivalently the Colts) measurements are all shifted by same amount where in reality each ball would be shifted by a different amount (Appeal p382 line 4-9; p 418 line 6-18; p438 line 14-21). Keeping the same average adjustment, the p-value slightly changes if there is a variable shift because of convexity. However, this effect is second order and changes the p-value by less than 10% and often increases the p-value in the variable adjustment scenarios I simulated. For example the 0.14 could become 0.13 or 0.15. Overall, this criticism is very weak since refining this analysis would only barely change the results and often increases the p-value.
They also argue that timing shouldn’t be included in this analysis (Appeal p 415 line 12-18; p 449 line 15-20), because there isn’t an order effect if the measurements are plotted in numerical order. This is a huge assumption! There could have been a large gap between the end of the Patriots measurements and the beginning of the Colts measurements. This definitely occurred if the Patriots footballs were inflated before the Colts measurements. Also, the footballs might not be numbered in the exact order of the measurements. The timing effect is definitely 0.3-0.4 psi, but the order analysis doesn’t incorporate the effect of a time gap and is extremely susceptible to even the smallest error in order recordings. Given the officials issues with switching gauges and measurements, the more robust analysis method should be preferred. To argue against timing effects in the analysis is to rely on real life events having fallen into a perfectly orderly pattern when it’s clear that they almost certainly didn’t. No timing effect would be a violation of the Ideal Gas Law; whereas, no order effect means the balls are not numbered in the exact measurement order. The timing analysis should trump the order analysis.
Finally, Exponent says that it is unknown exactly when the timing occurred (p449-450 line 21-ln 4). However, it is roughly known when the timing occurred; therefore scenarios can be developed for possible timings. This would allow estimation of the upper and lower timing effect on the statistical model. Since the Patriots’ footballs were measured before the Colts footballs, all timing scenarios would greatly increase the p-value.
Suppose you have several identical footballs with identical pressure. They are outside for the first half of a football game and then you take them inside for halftime. If you measure half at the start of halftime and second half at the end of halftime, then the identical footballs will show a statically significant difference (or nearly so) using the Exponent statistical model without a timing adjustment. If these identical footballs had the same variability as the Patriots-Colts footballs with a timing and wetness difference of 0.5 psi, then the p-value will be below 0.05. The Exponent model will incorrectly conclude identical footballs are statistically significantly different. The statistical model must include a timing term in order to give correct result.
“Preliminary” Analysis
Exponent sidesteps the criticism of its model by pointing out the finding with a 0.4% likelihood is simply part of the preliminary analysis. (Appeal p200-201, p360 line 1-5, p415 line 1-11; 454 line 7-14). If the Exponent report is read precisely, Exponent first performs a preliminary analysis to determine if further analysis is needed. It’s a rough and tumble model because it isn’t meant to be the final ruling, the argument goes. Besides the appeal testimony, this is mentioned in the Exponent report executive summary and conclusion (Exponent p X and p 64). This preliminary analysis doesn’t include any affect from timing, but the secondary analysis which follows does. However, the secondary analysis has a much, much weaker conclusion than the preliminary analysis.
Further, this doesn’t hold up outside of a very specific reading of the document as it exists, because the document was not wielded specifically by the NFL. Although the Exponent report states this result is preliminary, the Wells report doesn’t. This 0.4% likelihood is the central pillar of the Well’s report statistical argument against the Patriots. From page 114 of the Wells report:
According to both Exponent and Dr. Marlow, the difference in the average pressure drops between the Patriots and Colts footballs is statistically significant.
….
In fact, when the halftime measurements are attributed to the gauges most likely to have generated those measurements, there is only a 0.4% likelihood—a fraction of one percent—that the difference in average pressure drops between the teams occurred by chance.
As the Patriots showed, this is a completely false statement because it doesn’t include the timing effect. The Wells report mentions the weak conclusions from the rest of the Exponent report, afterwards, as minor support, but the 0.4% likelihood is the basis of their statistical argument. Therefore depending on how you slice it, either the Well’s report incorrectly quotes the Exponent report or the Exponent report contains incorrect analysis. However, either way the Wells report’s description of the statistical evidence against the Patriots is completely incorrect. The 0.4% likelihood number is simply wrong. Even, Exponent wasn’t willing to stand behind this number, saying it was only preliminary. (Appeal p200-201, p360 line 1-5, p415 line 1-11; 454 line 7-14)
Exponent’s Secondary Argument
Chronologically, Exponent first performs the preliminary analysis and then discovered that the timing factor is important and explores it in detail. (Appeal p360 ln 1-25). However, Exponent decides not to update the preliminary analysis to include this factor. Instead, Exponent decides to change from analyzing the difference between the Patriots and Colts pressures to analyzing if the Patriots halftime pressures are plausible on their own. They determine the preliminary study flawed because it doesn’t include the timing effect, but don’t follow up by including it. It’s a perplexing, circuitous way to see if the timing effect can explain the incomplete preliminary finding. (Appeal p205-206 quotes Exponent p 43)
Determining the absolute theoretical pressures for the footballs is a much more complicated problem because the absolute pressure value depends on many unknown assumptions involving time, temperature, wetness and gauge usage. Exponent reproduces numbers consistent with the Patriots measurements, but only with assumptions they feel are unlikely. This conclusion is not presented in a statistical framework and there is no probability or statistical significance associated with this conclusion. They simply provide plots and say the Patriots measurements are unlikely, they guess, basically.
No one has been discussing this part of the Exponent report because it involves non-statistical hand waving and the conclusion is extremely weak. However, the since Exponent is claiming that their statistical model is only preliminary; then the final analysis should be discussed. Exponent is probably overestimating the temperature of the locker room at the beginning of halftime. The locker room is temperature controlled, but at halftime the stadium doors are completely opened; several hundred people walk inside; and they must bring a lot of cold air with them. A few degrees change the calculations of the theoretical pressure. Also, if the Patriots footballs are re-inflated before the Colts footballs are measured, then Colts sample point average times of 7:10, 8:15, 9:14 seem way too early and the Colts measurements don’t seem very believable either. Overall, the secondary analysis seems to exist so Exponent can claim that they incorporated the timing effect in their analysis. But there is nothing that can be considered a statistical proof.
Why this matters
Whether or not Tom Brady and the Patriots actually tamper with their balls or attempted to do so doesn’t actually matter here. What we’re looking at, in the absence of red-handed guilt, is the NFL, its investigatory arm, and that arm’s hired experts railroading an investigation with shoddy, biased works of bad science, and then holding up their homework to Roger Goodell, who sticks a gold star on it and calls it “highly credible.” It’s a work. And as long as the NFL continues to pretend that its commissioner issues judicious opinions from his seat at the head of the court, league cronies will be forced to gin up enough evidence-like substances to work the courts.
Jason Cohen has a PhD in Applied Probability and Statistics from Cornell University and works in quantitative finance. You can follow him on Twitter @ jasonicohen.
Baker Mayfield Can't Stop Talking About the Cleveland Browns
The Three Biggest 2026 NBA All-Star Starter Snubs
Why John Harbaugh Is Exactly What the New York Giants Needed
Why the Detroit Lions’ Drew Petzing Hire Makes No Sense
- Sunday January 18th College Basketball Betting Picks, Predictions
- Houston Texans vs. New England Patriots NFL Playoffs Betting Picks, Predictions
- NFL Divisional Round 2026 Best Bets, Picks, Predictions
- Buffalo Bills vs. Denver Broncos Divisional Round Betting Picks
- Top NBA Betting Picks Tonight: Clippers-Raptors, Wolves-Rockets, Wizards-Kings
- Thursday Jan. 16 NHL Betting Picks: Lightning vs. Blues, Panthers vs. Hurricanes
- Thursday NBA Betting Picks: Three Best Bets Before a Big Sports Weekend












